01

簡 介 

約束作為多體動力學的基本要素，應用在每個模型中。本文對軟件界面的約束及其對應的代數方程進行整理說明，以期更好的應用軟件。

約束可以分為定常約束（與時間無關的）和非定常約束（與時間相關的）。又可以分為完整約束（對位移進行約束）和非完整約束（對速度進行約束）。不同的分類應用在不同的分析場景，本文只對空間定常約束，即大家熟悉的固定副、球副、圓柱副、移動副、旋轉副、萬向副、平行副、垂直副進行說明。

02

約束的代數方程 

固定副

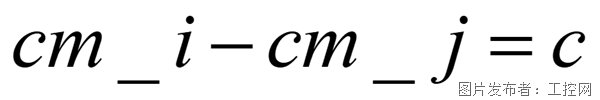
即部件j的質心與部件i的質心位置/角度的差值是個常數。

球副

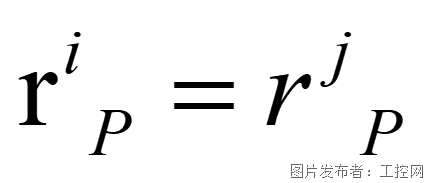
全局坐標系下，部件i與部件j的這兩個點位置始終重合，從而使部件j不能與部件i有相對運動，即限制了部件j的三個移動自由度。

圓柱副

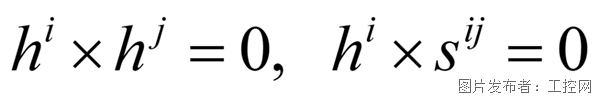
第一項，部件i與部件j上的兩個向量一直平行，限制了部件j繞部件i兩個方向的轉動（若是部件j能夠相對轉動，那么初始平行的兩個向量就不滿足平行關系）；第二項，部件i上的向量與約束軸線平行，限制了部件j的兩個移動（若是部件j朝著其他方向移動，那么sij與hi將不再平行）。

移動副

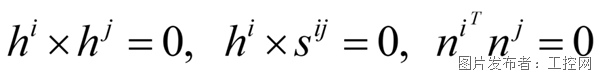
在圓柱副的基礎上再加第三項，額外限制旋轉，ni與nj分別是在部件i與部件j上的兩個向量，相互垂直，且都垂直于約束軸線。（若是部件j轉動，那么兩個向量將不滿足垂直關系）

旋轉副

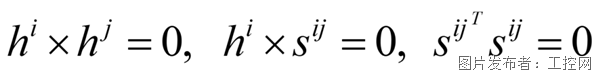
在圓柱副的基礎上再加第三項，額外限制移動，及sij在這個方向的投影一直是0，或者一個常數。

萬向副

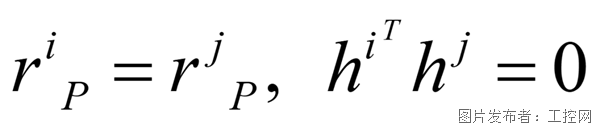
球副的基礎上再額外限制旋轉。（道理同移動副的第三項）

向下滑動查看

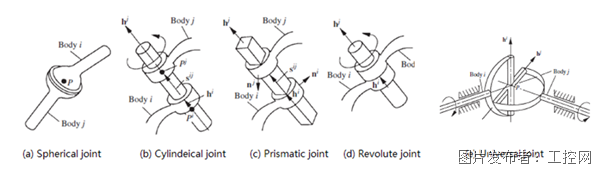
圖1 常見約束副

表1 約束公式匯總

從上表也可以看出，旋轉副也可以用一個球副疊加限制兩個旋轉自由度的平行副： 

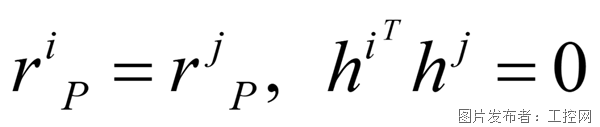
也可以看出垂直副、平行副是基礎副，其他約束可以用其來構造。

03

 萬向副的驗證 

萬向副由于其約束關系，存在不等速的特性。本節(jié)通過Matlab與Adams分別建立模型，驗證此特性。

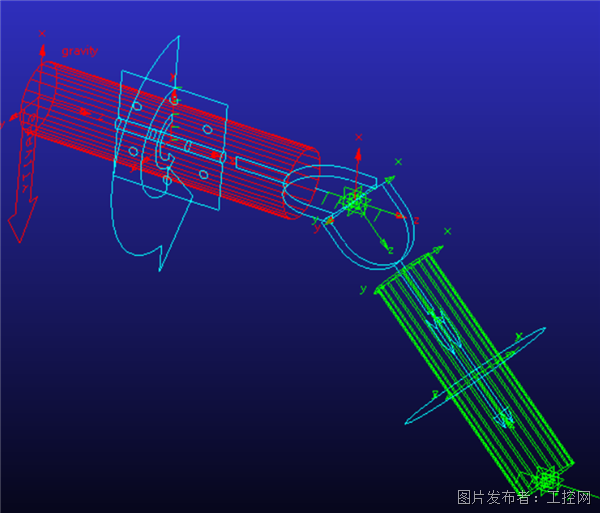
圖2 萬向副驗證模型

在Adams中創(chuàng)建部件i（紅色圓柱），部件j（綠色圓柱），部件i與大地旋轉副約束，并施加60deg/s的恒定角速度驅動；部件j與大地平行副約束，部件j與部件i萬向副約束。

在Matlab中，采用相同的約束。

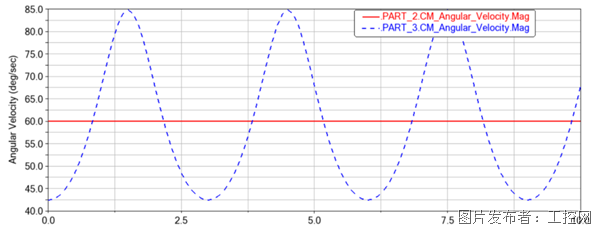
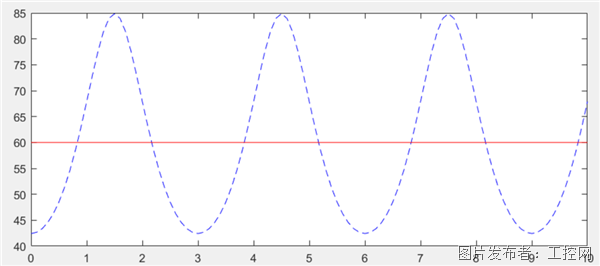
圖3 Adams結果VS Matlab結果

兩者結果完全一樣，驗證了上述旋轉副、萬向副及平行副的代數方程。

04

參考文獻 

[1] computational Dynamics (3rd). Ahmed A. Shabana.